The way designspaces work is not always very intuitive. GX started these ideas. MutatorMath implemented some of them. VariationModel does too. But this is the result of the nature of the thing and there is not much point in debating it. For a more detailed description of how the factors are calculated, see MutatorMath: DesignSpace Factors. There is a also a lecture on how the factors work on vimeo. But I can try to explain some of the effects of non-aligned masters in a 2 dimensional space.
The color maps in this post were generated with Drawbot using VariationModel from fontTools.varLib.models. Rather than font data, this example processed (r, g, b) values. This visualises the extent of the effect of each master and also illustrates how different masters are added up to make instances.

Here is a two axis, 4 master system. The master M0, colored red is the origin, the connection of all axes. The vertical axis runs from origin M0 to on-axis master M1, colored yellow. The horizontal axis runs from M0 to on-axis master M2, white. Master M3, black, is an off-axis master that aligns with master M1 and master M2.
Adding masters on-axis or off-axis makes a big difference. The factors are calculated differently. Let's have a look at adding an on-axis master, and, in a different example, adding an off-axis master.
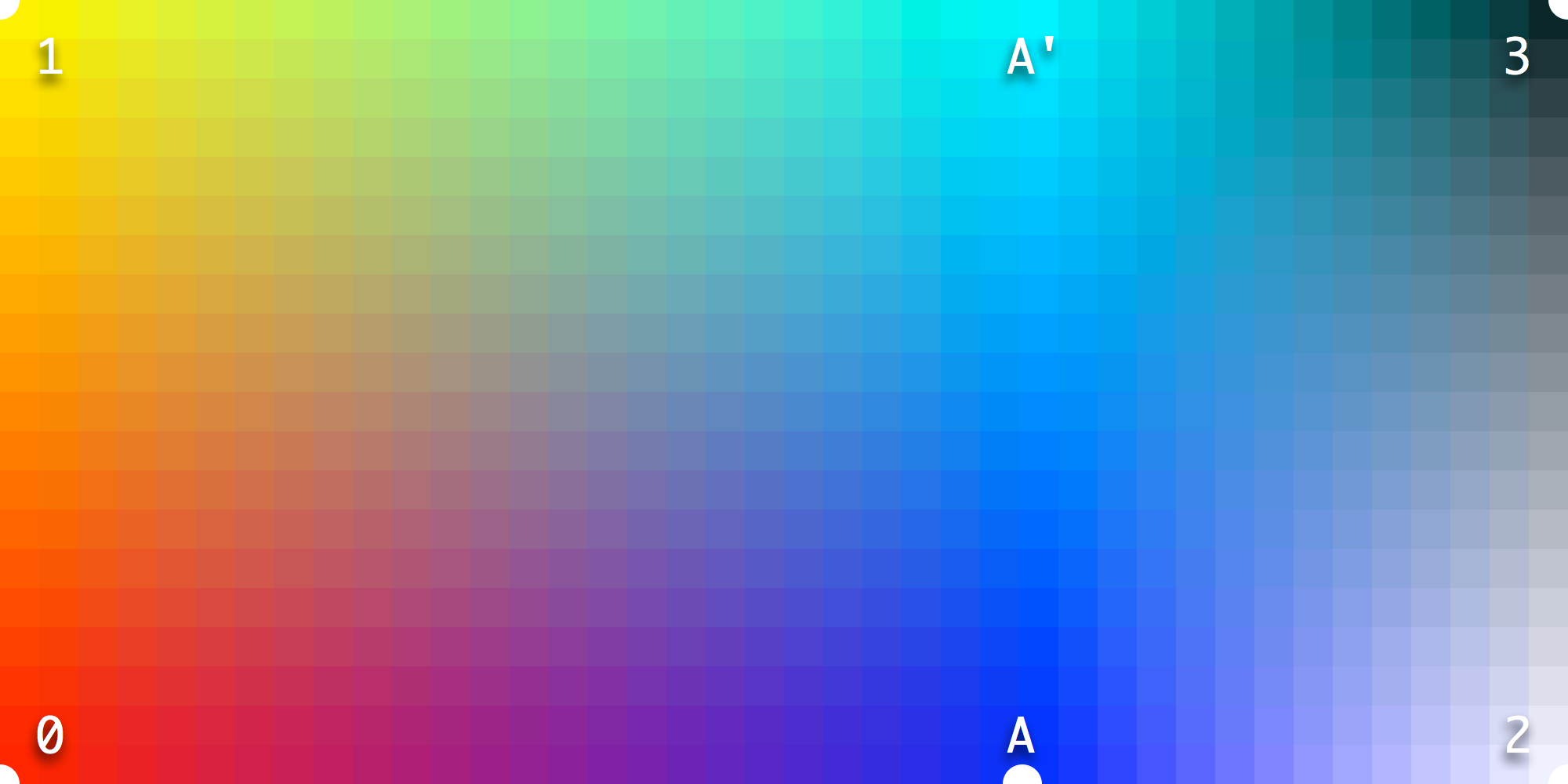
We add a blue on-axis master MA that aligns with origin master M0 and on-axis master M2.
At location A', between M1 and M3, the gradient from yellow to black has been interrupted, the map has become cyan. This is not a color present in any of the masters, so what's going on here? Because master MA is on-axis, its influence is not limited by master M1 or master M0. The #00F color is at full blast. However, #F00 from master 0 at the origin is also present. #00F + #F00 = #F0F, hence cyan. But it is an unexpected result that needs to be addressed.
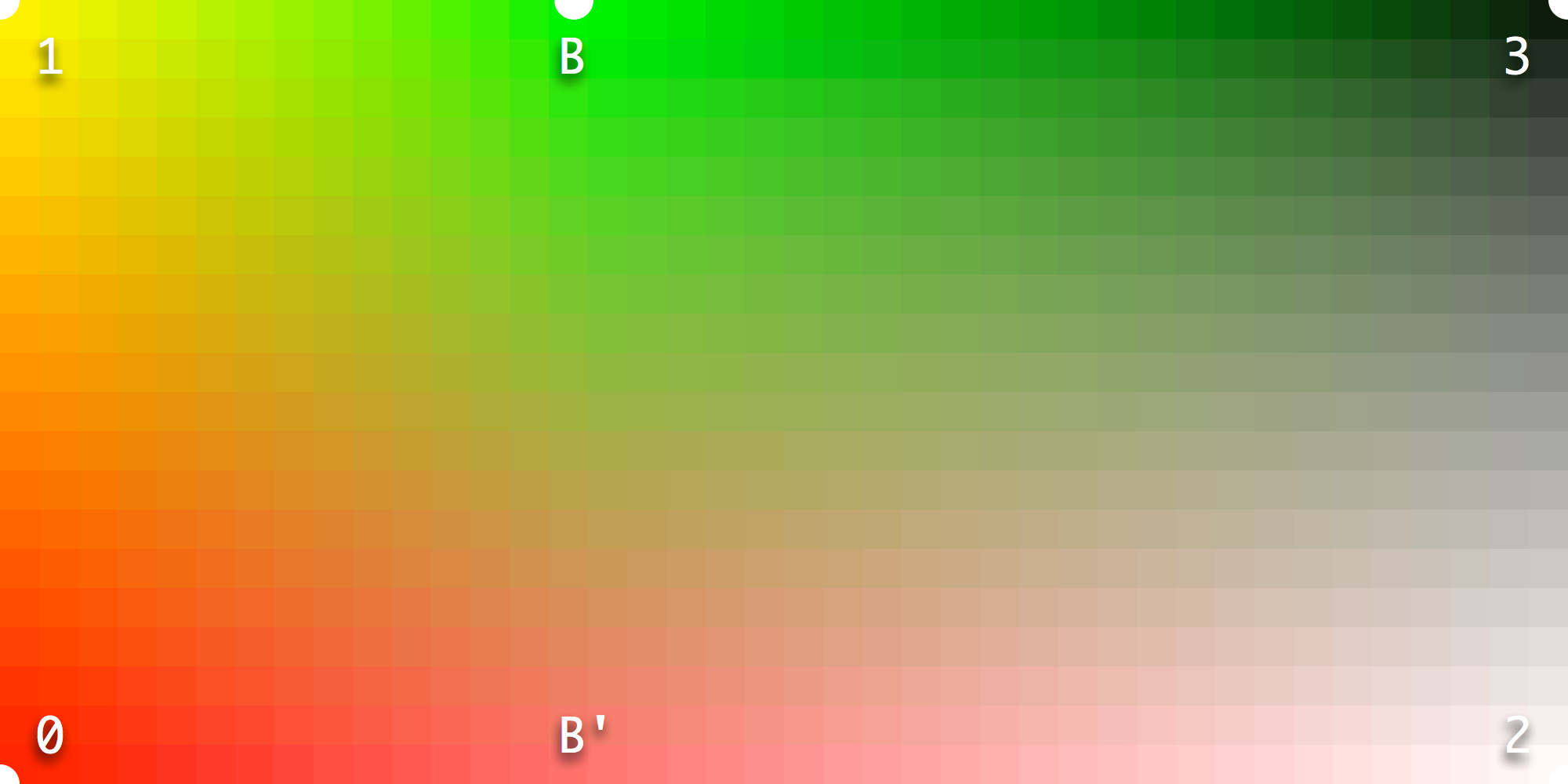
Alternatively, if we add a master MB, colored green, between M1 and M3, we observe the interpolation between M1 and M3 is interrupted. But at B', unlike A' in the previous example, the interpolation between M0 and M2 is not interrupted.
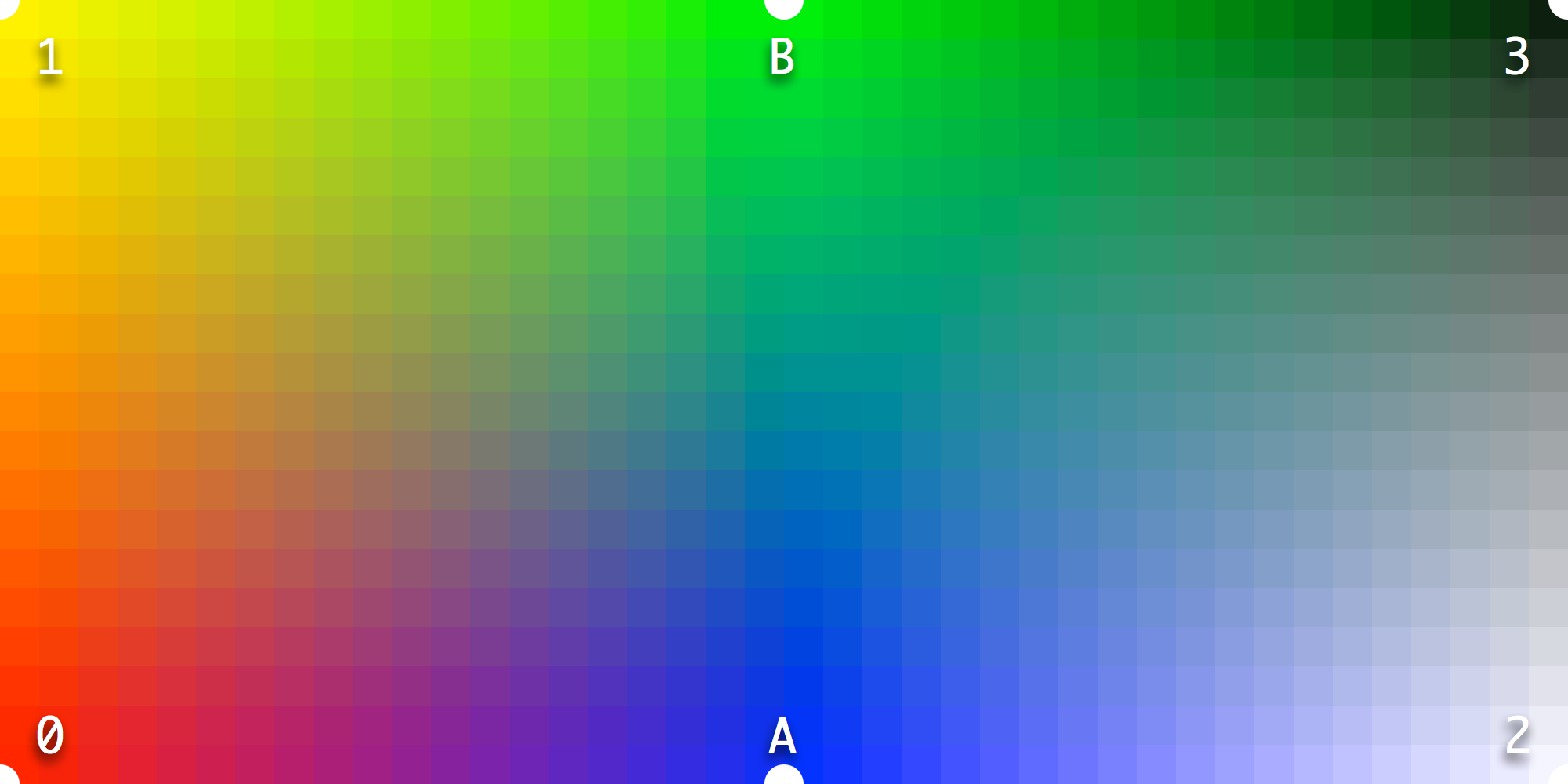
In this example we add both MA and MB masters, with the same coordinate on the M0-M2 axis. We don’t see the cyan from example 2.1.
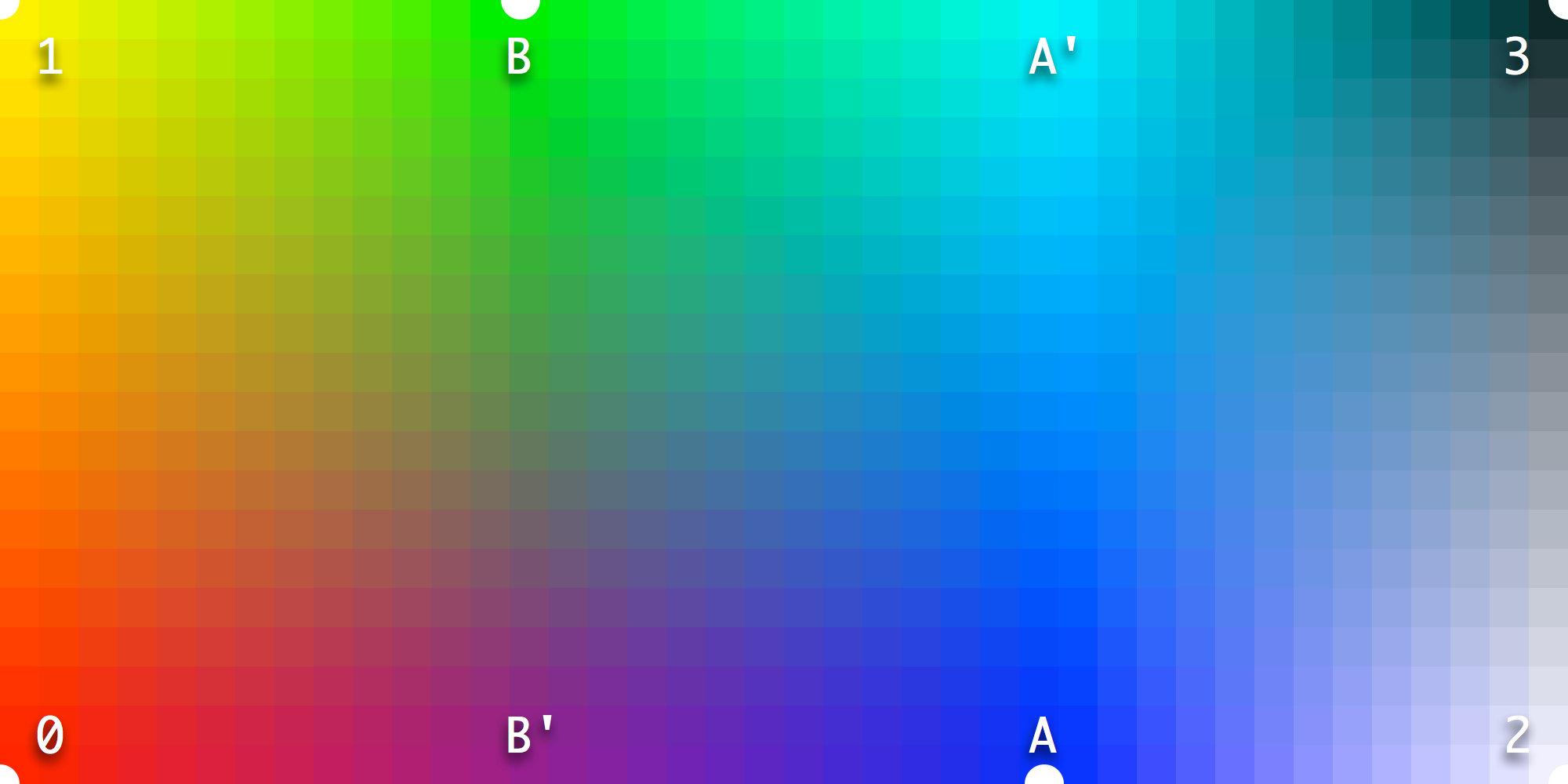
In this example we add both MA and MB masters, with the different coordinates on the M0-M2 axis. As with example 2.1, on-axis master MA limits the influence of off-axis master M3 along the M0-M2 axis. It also limits the influence of MB. So at A' we see cyan. At B' nothing special happens, M0-MA is not interrupted and the influence of MB is 0. So we see the mix of M0 and MA, purple.
So how do we resolve a system with non-aligned masters MA and MB? It is clear that the designspace does not give an intuitive answer.
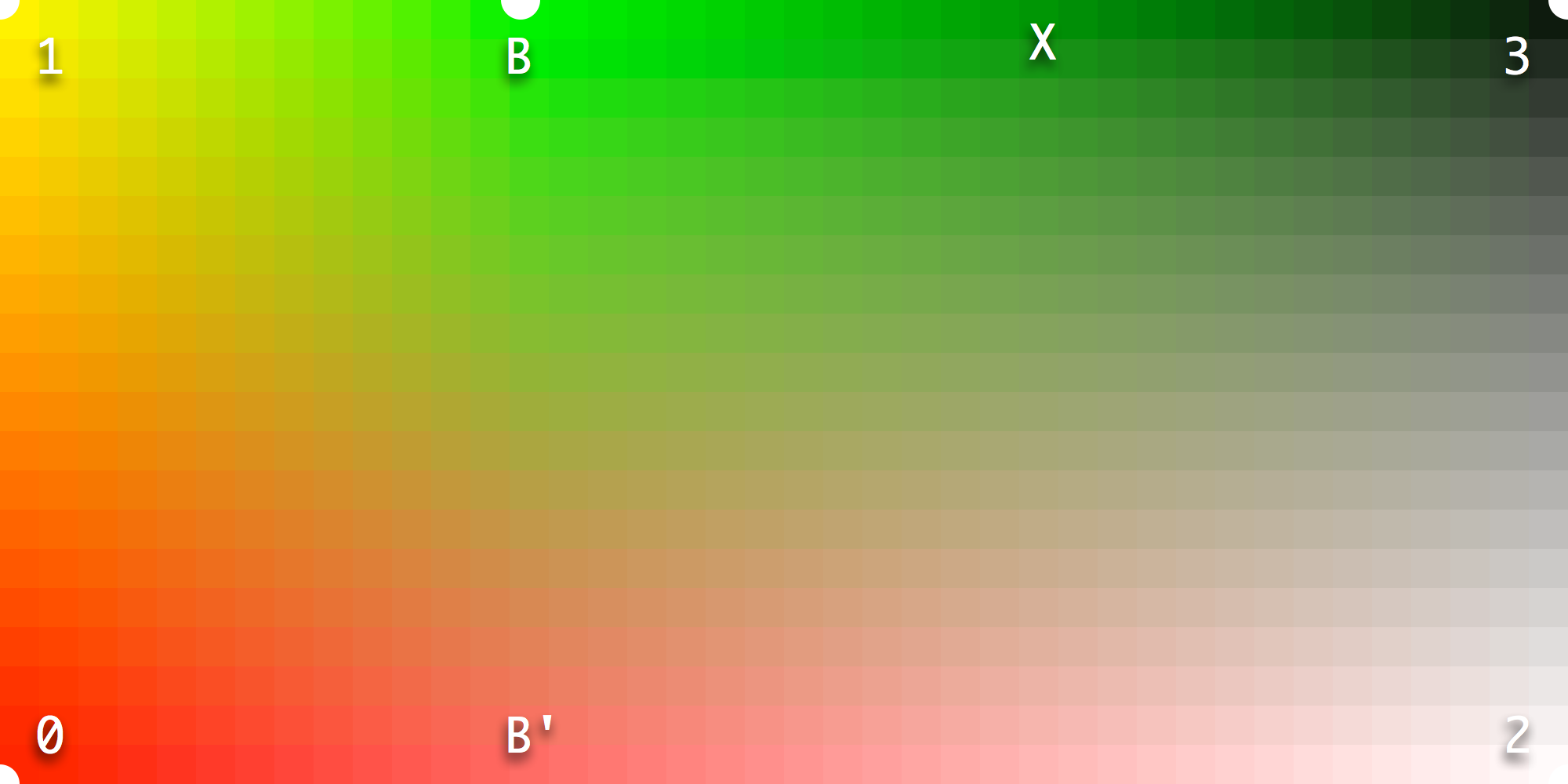
If we return to the map of example 2.2, with the off-axis master MB added between M1 and M3. We can calculate the color at X (the location of A' from example 2.4), a dark green, what we would expect from an interpolation between a bright green at MB and black at M3.
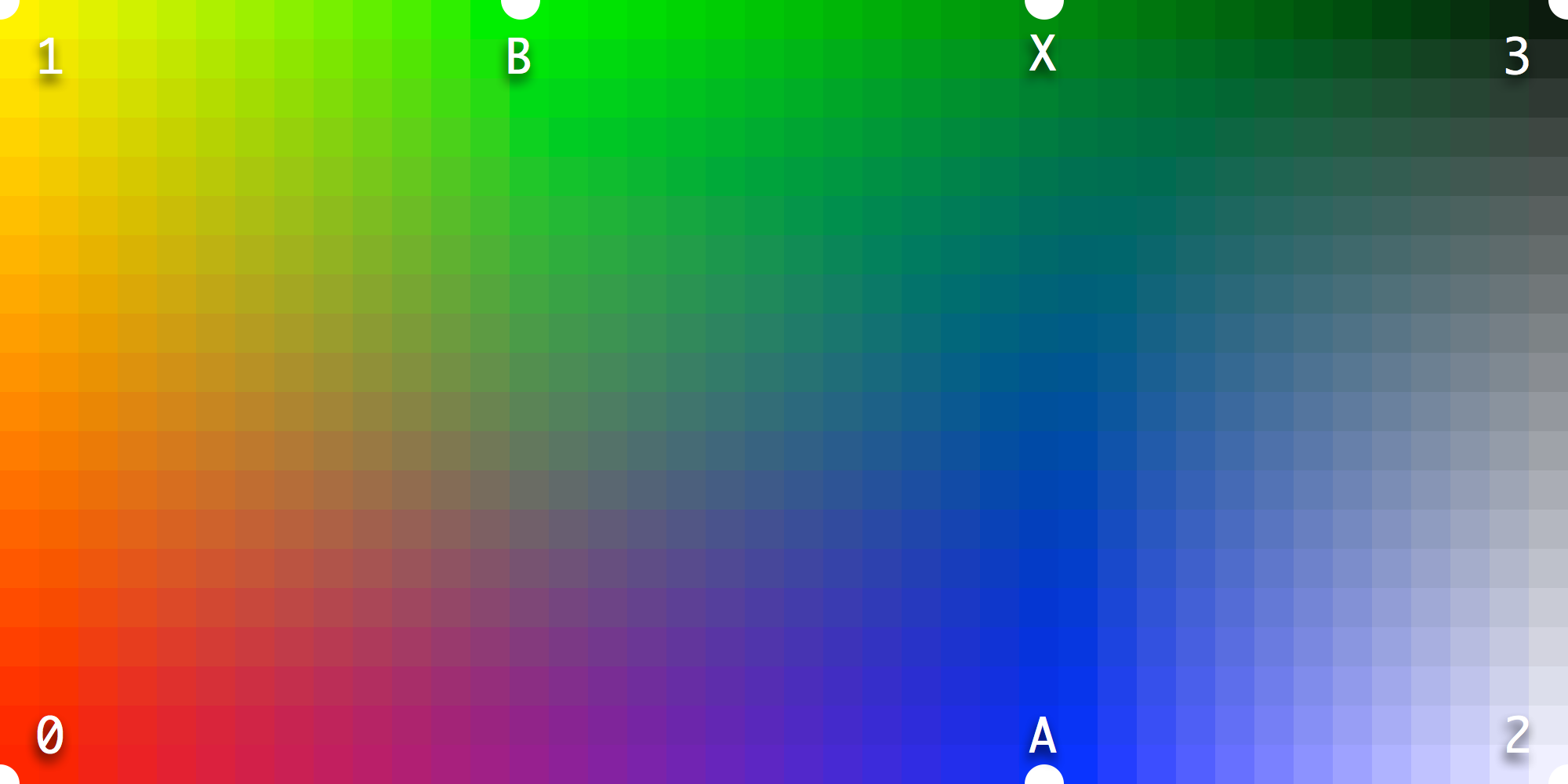
The sampled results from location X are inserted as a new master, MX that aligns with MA. The off-axis effects of MA are no longer visible. The results along M1-MB-MX-M3 are as expected. The results along M0-MA-M2 are also as expected. If VariationModel is used then adding a single support master at location MX should be enough.
However, there are some differences between MutatorMath and VariationModel. The latter has a more complete algorithm for sorting non-aligned masters. If we superimpose the last map with the results generated with MutatorMath drawn in circles, it is clear that there are some differences. Around M0 and MA the map is undefined. Aha you say! Are these the differences we see? No. The differences you see are in example 3. Solving the differences in example 5 would be nice but it won't fix the other problems.
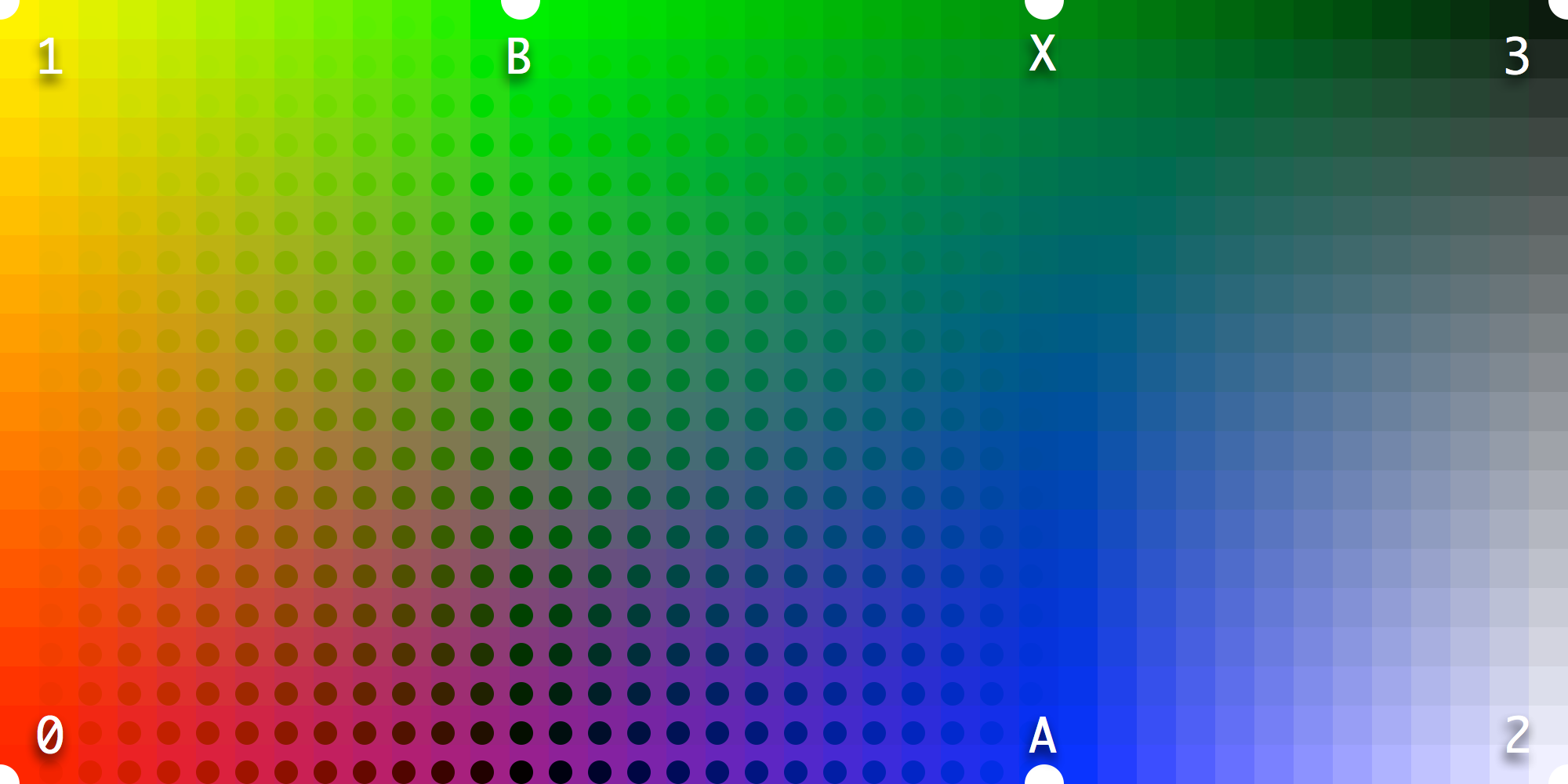
The easiest solution is to sample the wanted results at location B' and then insert those as a new master at MY. The differences between MutatorMath and VariationModel are gone again.
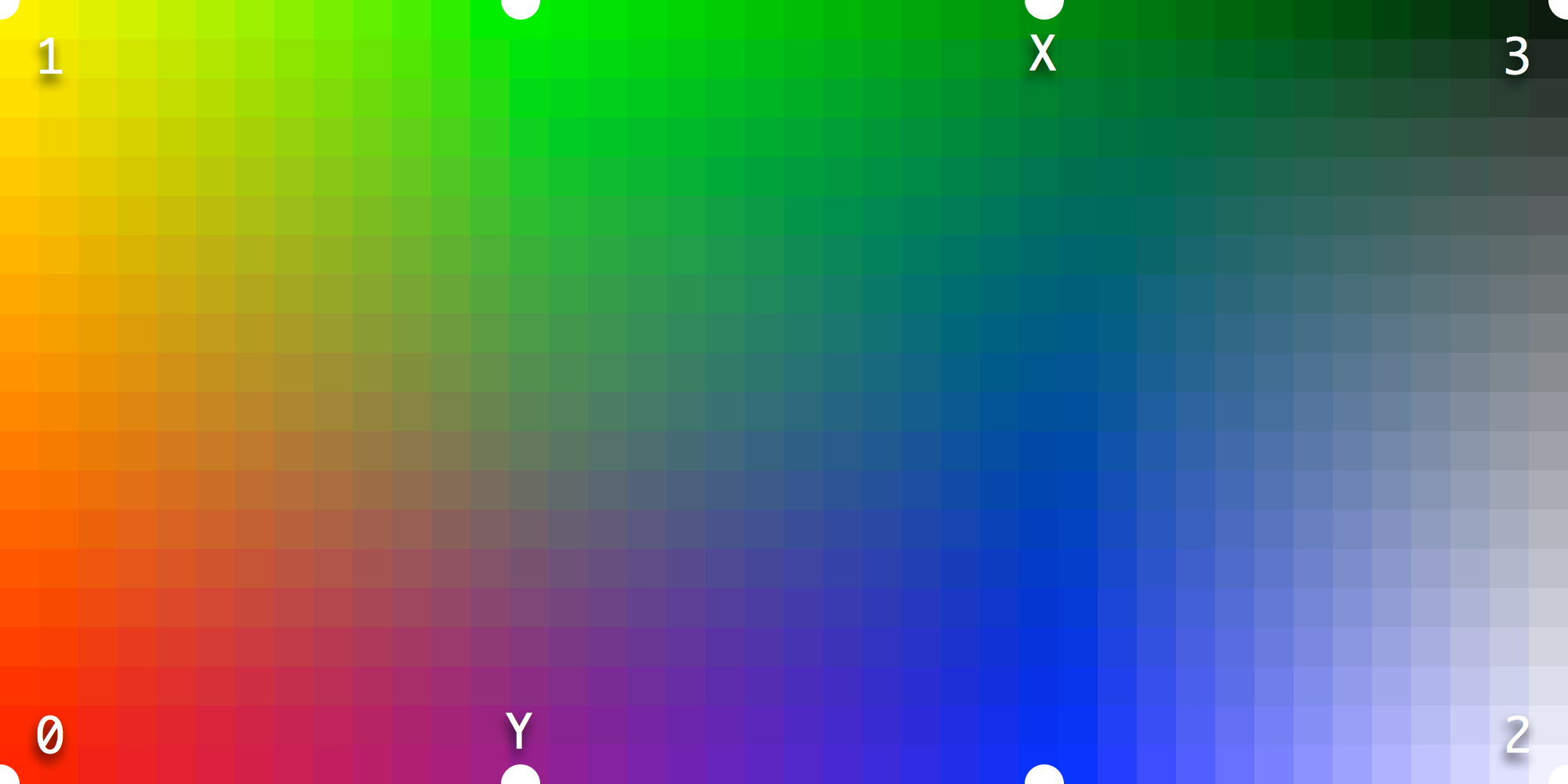
By adding extra supports the designspace can be fixed. This can be done using MutatorMath or with VariationModel.
VariationModel can be used to calculate instances, just like MutatorMath. It might need some work on the code that builds the UFOs, but then it should be enough to just add MX. There are different ways in which VariationModel could be folded into the generating process.
Version 1: 2017 March 21
Version 2: 2022 September 28. Recreated with html from archive.org and images from my archive. No edits to the text.